BucketCTF 2023 Writeup

Finished as 55th out of 709, with 19 flags and 5428 points.
Writeup for BucketCTF 2023 challenges:

• Maze (478 Points, HARD)
• Random Security (452 Points, MEDIUM)
• Tetris (364 Points, MEDIUM)
• Search 1 (390 Points, MEDIUM)
• Search 0 (380 Points, EASY)

Maze (478 Points, HARD)

The maze challenge was an interesting one that required understanding of Java’s pseudorandom number generator.

The challenge provides a maze.class file that implements the behaviour in their server.
We can view the file using JD-GUI to see the decompiled Java source code.

The source code shows two important methods defined in the Maze class.

• initMap(), which initializes the maze that we have to escape
• main(), which handles the game logic and user movement etc.

Take a look at the main() function:

public class Maze {

  public static char[][] maze;
  public static Random random = new Random();

  public static void main(String[] paramArrayOfString) {
    initMap();
    byte b1 = 20;
    byte b2 = 20;
    try {
      Scanner scanner = new Scanner(System.in);
      while (true) {
        char c = scanner.next().charAt(0);
        if (c == 'Q') {
          if (maze[b1 - 1][b2 - 1] == '#')
            break; 
          maze[b1][b2] = ' ';
          maze[--b1][--b2] = 'X';
        } 
        // ...
        // Code that handles movement in the maze
        // ...
        if (c == 'A') {
          if (maze[b1][b2 - 1] == '#')
            break; 
          maze[b1][b2] = ' ';
          maze[b1][--b2] = 'X';
        } 
        if (c == 'R')
          System.out.println("Here is a random number for you since i'm nice: " + random.nextDouble()); 
      } 
      scanner.close();
      System.out.println("YOU LOSE I WIN! BETTER LUCK NEXT TIME!");
    } catch (Exception exception) {
      if (exception instanceof ArrayIndexOutOfBoundsException)
        System.out.println(getFlag()); 
    } 
  }
}

The main() function initializes the map, and sets the player’s position to (20, 20) which is the center of the maze. Then it allows the user to move the player in 8 different directions using the keyboard: (Q - NorthWest, W - North, E - NorthEast, A - West, D - East, Z - SouthWest, S - South, C - SouthEast). In addition to these keys, the program also accepts the key R, and provides the user with a random Double.

Lastly, the flag is printed out if there is an ArrayIndexOutOfBoundsException. This means that we have to move out of one of the edges of the maze, and escape it.

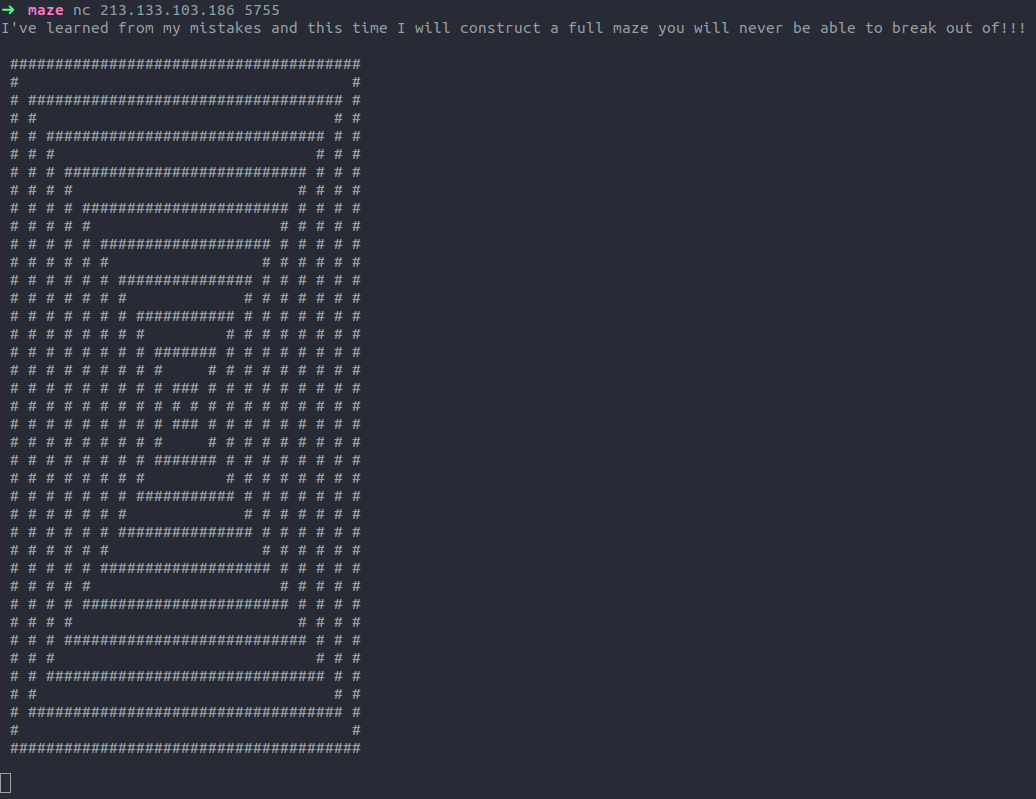
Keeping this in mind, let’s check how the maze is contructed:

  public static void initMap() {
    System.out.println("I've learned from my mistakes and this time I will construct a full maze you will never be able to break out of!!!");
    maze = new char[41][41];
    byte b;
    for (b = 1; b <= 20; b++) {
      if (b % 2 == 1)
        for (int i = 20 - b; i <= 20 + b; i++) {
          for (int j = 20 - b; j <= 20 + b; j++) {
            if (i == 20 - b || i == 20 + b || j == 20 - b || j == 20 + b)
              maze[i][j] = '#'; 
          } 
        }  
    } 
    for (b = 0; b < maze.length; b++) {
      for (byte b1 = 0; b1 < (maze[b]).length; b1++) {
        if (maze[b][b1] != '#')
          maze[b][b1] = ' '; 
        System.out.print(maze[b][b1]);
      } 
      System.out.println();
    } 
    for (b = 0; b < 10; b++) {
      int i = 3 + b * 4;
      int j = random.nextInt(i);
      int k = random.nextInt(4);
      switch (k) {
        case 0:
          maze[20 + i / 2][20 - i / 2 + j] = ' ';
          break;
        case 1:
          maze[20 - i / 2 + j][20 + i / 2] = ' ';
          break;
        case 2:
          maze[20 - i / 2][20 - i / 2 + j] = ' ';
          break;
        case 3:
          maze[20 - i / 2 + j][20 - i / 2] = ' ';
          break;
      } 
    } 
    maze[20][20] = 'X';
  }

The maze is built with # square walls placed in each odd numbered row/column. Then, in each square wall a hole is randomly placed to allow players to escape. This is done by choosing two random numbers j and k, using random.nextInt(bound) If we can find out what the values of j and k were, we would be able to find the escape route.

After searching up how to predict the random numbers generated using Java.Util.Random, I found a very helpful post that explained exactly this.

The Java.Util.Random source code shows that it uses a Linear Congruential Generator that is easy to predict, if you can get two values generated by the Random object.

A Linear Congruential Generator uses a starting seed X, and generates the next seed X₁ with

X₁ = ( a * X + c ) mod m

But that also means that we can find the original seed X with

X = ((X₁ - c) * a^-1) mod m

if a has a modular inverse in mod m.
Java.Util.Random uses the values:

• a (multiplier) = 0x5DEECE66D
• c (addend) = 0xB
• m (mask + 1) = 0x1000000000000 (or 2⁴⁸)

Thankfully, a and m are coprime, which means a does have a modular inverse and the previous seed can be calculated. Since we can get a random double generated from the server using R key, we can probably get the original seed of the server’s Random object and predict all the other pseudorandom numbers generated in the server.

But how is the seed used to generate the random double or random ints? Here is how Java does it but in python, for ease of understanding:

multiplier = 0x5DEECE66D
addend = 0xB
mask = (1 << 48) - 1

def next(n):
    global seed
    seed = (seed * multiplier + addend) & mask
    return seed >> (48 - n)

def nextDouble():
    return ((next(26) << 27) + next(27)) / (1 << 53)

def nextInt(bound):
    r = next(31)
    m = bound - 1
    if (bound & m) == 0:    # if bound is a power of two
        r = (bound * r) >> 31
    else:
        u = r
        r = u % bound
        # Some checks to see if random number becomes negative from overflow?
        while u - r + m > (1 << 31) - 1:
            u = next(31)
            r = u % bound
    return r

Notice that modulo 2ⁿ is equivalent to taking the lower n bits of the number, hence the mask = (1 << 48) -1 . nextDouble() and nextInt(bound) are both implemented using next(n), which calculates a new seed and uses the lower n bits of the new seed. Since next(n) directly uses the lower n bits of the seed, the generated values contain the bits of the internal seed (parts of it). Also, as nextDouble() wants 53 bits when the seed is only 48 bits long, it calls next() twice. Once to get the top 26 bits, once to get the bottom 27 bits. Therefore one random double value contains information about two consecutive seeds, which are related by the equation of the Linear Congruential Generator mentioned above. The remainder of the bits can then be brute forced easily to find the seed:

double = float(input("Input the float > "))

num = int(double * (1 << 53))
first_seed_top = num >> 27
second_seed_top = num & ((1 << 27) - 1)

for i in range(1 << 22):
    global seed
    first_seed = (first_seed_top << (48 - 26)) + i
    if ((first_seed * multiplier + addend) & mask) >> (48 - 27) == second_seed_top:
        seed = (first_seed * multiplier + addend) & mask
        print(f"FOUND: {first_seed}")

Using this script, we can find the interal seed of the Random Object in the server. Now, we have to find the values of Random.nextInt(bound) that were generated previously. Looking at the code, next(31) is called only once. There is a while loop that could call next(31) again if an overflow occurs?, but this part of the code is never called because the value for the bound used is small in our case. Therefore every call to nextInt(bound) would have generated a new seed exactly once. nextInt(bound) is called in the program twice for every hole generated, and there are 10 square walls. We can revert the seed value to the first value by calling prev_seed() 20 times. We also call prev_seed() twice at the start to account for the random double value we generated.

from Crypto.Util.number import inverse

inv = inverse(multiplier, mask + 1)

def prev_seed():
    global seed
    seed = (((seed - addend) & mask) * inv) & mask

prev_seed()
prev_seed()
for i in range(20):
    prev_seed()

Now we can locally generate an exact copy of the maze, using the same code logic from maze.class, to visualize the escape route.

for b in range(1, 21, 2):
    for i in range(20 - b, 21 + b):
        for j in range(20 - b, 21 + b):
            if i == 20 - b or i == 20 + b or j == 20 - b or j == 20 + b:
                maze[i][j] = '#'

for b in range(10):
    i = 3 + b * 4
    j = nextInt(i)
    k = nextInt(4)
    if k == 0:
        maze[20 + (i // 2)][20 - (i // 2) + j] = ' '
    if k == 1:
        maze[20 - (i // 2) + j][20 + (i // 2)] = ' '
    if k == 2:
        maze[20 - (i // 2)][20 - (i // 2) + j] = ' '
    if k == 3:
        maze[20 - (i // 2) + j][20 - (i // 2)] = ' '

maze[20][20] = 'X'
for row in maze:
    print("".join(row))

I have also implemented the movement which helped me to keep track of where my player is at.

x = 20
y = 20
while True:
    string = input()
    maze[x][y] = ' '
    for c in string:
        if c == 'Q':
            x -= 1
            y -= 1
        # ...
        if c == 'C':
            x += 1
            y += 1
    maze[x][y] = 'X'
    for row in maze:
        print("".join(row))

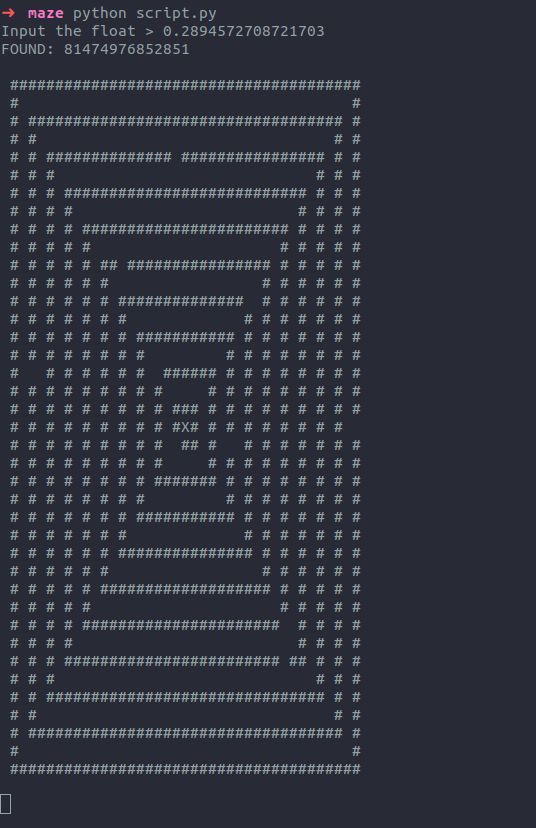
With this, we can finally escape the maze and get our flag

Flag: bucket{r4nd0m_n3v3r_w0rk5_e92fc72d}

Random Security (452 Points, MEDIUM)

The challenge only provided a port to connect to. Here is the description of the challenge

One of my friends recently learned Java and started teasing all of us for not knowing anything about programming. He made what he called a secure program and challenged us to steal some flag from it. I have no idea where to even start, could you help out?

If you read the Maze Writeup directly above, this is a very similar problem that requires us to predict a pseudorandom number generated by Java.Util.Random.

The challenge server gives us a random double, and wants us to give it one, too. A reasonable guess is that if we can predict the next random double, we will be able to get the flag. Using the previous code, we generate the random double and get the flag.

multiplier = 0x5DEECE66D
addend = 0xB
mask = (1 << 48) - 1

double = float(input("Input the float > "))

num = int(double * (1 << 53))
first_seed_top = num >> 27
second_seed_top = num & ((1 << 27) - 1)

for i in range(1 << 22):
    global seed
    first_seed = (first_seed_top << (48 - 26)) + i
    if ((first_seed * multiplier + addend) & mask) >> (48 - 27) == second_seed_top:
        seed = (first_seed * multiplier + addend) & mask
        print(f"FOUND: {first_seed}")

def next(n):
    global seed
    seed = (seed * multiplier + addend) & mask
    return seed >> (48 - n)

def nextDouble():
    return ((next(26) << 27) + next(27)) / (1 << 53)

print(nextDouble())

Flag: bucket{RaNd0m_nUmb3r5_53cur3_d24d8c961}

Tetris (364 Points, MEDIUM)

This was a typical equation solving challenge, which can be solved using solvers like z3. A tetris.jar file is provided, which we decompile and view using JD-GUI. We find a retFlag() function, which is of the most interest to us. The grid variable refers to the tetris grid, with 20 rows and 10 columns. Let’s check the first part of the function

public String retFlag() {
    String[] arrayOfString = new String[25];
    byte b1 = 1;
    String str1 = "";
    byte b2;
    for (b2 = 0; b2 < this.grid.length; b2++) {
      for (byte b = 0; b < (this.grid[0]).length; b++) {
        if (this.grid[b2][b] != null) {
          str1 = str1 + "1";
        } else {
          str1 = str1 + "0";
        } 
        if (b1 % 8 == 0) {
          arrayOfString[b1 / 8 - 1] = str1;
          str1 = "";
        } 
        b1++;
      } 
    } 

The strings are created by checking if each position in the tetris grid has a tetris block present or not. So if the tetris blocks were in some specific configuration, the flag would have been printed out. The grid is 20x10 = 200 positions, and each position corresponds to a bit. 8 bits make a byte or a character, and 200 / 8 = 25 which matches the length of the string array. The next part of the function shows the criteria for the flag

    b2 = 0;
    boolean bool1 = false, bool2 = false, bool3 = false, bool4 = false, bool5 = false, bool6 = false, bool7 = false, bool8 = false, bool9 = false, bool10 = false, bool11 = false, bool12 = false, bool13 = false, bool14 = false;
    int[] arrayOfInt = new int[25];
    int i;
    for (i = 0; i < arrayOfString.length; i++)
      arrayOfInt[i] = Integer.parseInt(arrayOfString[i], 2); 
    i = 0;
    for (byte b3 = 0; b3 < 8; b3++)
      i += arrayOfInt[b3]; 
    if (i == 877)
      b2 = 1; 
    if (arrayOfInt[13] == arrayOfInt[16] && arrayOfInt[13] == arrayOfInt[21])
      bool1 = true; 
    if (arrayOfInt[19] == 7 * (arrayOfInt[12] - arrayOfInt[13]) / 2)
      bool2 = true; 
    if (arrayOfInt[13] + arrayOfInt[12] == arrayOfInt[16] + arrayOfInt[15])
      bool3 = true; 
    if (arrayOfInt[7] + arrayOfInt[8] + arrayOfInt[9] - 51 == 2 * arrayOfInt[9])
      bool4 = true; 
    if (arrayOfInt[8] == arrayOfInt[20])
      bool5 = true; 
    if (arrayOfInt[10] + arrayOfInt[11] - arrayOfInt[17] - arrayOfInt[18] == arrayOfInt[10] - arrayOfInt[17])
      bool6 = true; 
    if (arrayOfInt[20] == 51)
      bool11 = true; 
    if (arrayOfInt[22] + arrayOfInt[23] == arrayOfInt[22] * 2)
      bool7 = true; 
    if (arrayOfInt[9] - arrayOfInt[17] == 40)
      bool12 = true; 
    if (arrayOfInt[10] - arrayOfInt[17] - 6 == 0)
      bool13 = true; 
    if (arrayOfInt[2] - arrayOfInt[11] == 50)
      bool10 = true; 
    if (arrayOfInt[24] - arrayOfInt[12] == 10)
      bool14 = true; 
    if (arrayOfInt[13] + arrayOfInt[15] == 2 * arrayOfInt[14])
      bool8 = true; 
    if (arrayOfInt[23] == arrayOfInt[22] && 3 * arrayOfInt[23] == arrayOfInt[2])
      bool9 = true; 
    String str2 = "";
    for (byte b4 = 0; b4 < arrayOfInt.length; b4++)
      str2 = str2 + (char)arrayOfInt[b4]; 
    if (b2 != 0 && bool1 && bool2 && bool3 && bool4 && bool5 && bool6 && bool7 && bool8 && bool9 && bool11 && bool12 && bool13 && bool10 && bool14)
      return "correct flag: " + str2; 
    return "wrong flag: " + str2;
  }

We can copy this over to a python script that uses z3 to solve for the values. However, when run, the solution given by z3 will not be correct. There are multiple possible solutions to this set of equations. At first, I thought that we needed to be extra clever, using extra information that tetris blocks cannot float around, which means if some bit was set due to a tetris block being present in that position, one of the consecutive bits (up, down, left or right) must also be set, which is reflected in other bits of other strings. However, after the ctf ended, it was revealed that this was just a mistake from the problem setter. During the ctf, I just solved for all possible values, and it was obvious which solution was the flag.

from z3 import *

flag = [Int(f"flag[{i}]") for i in range(25)]

known = "bucket{"
for i in range(len(known)):
    flag[i] = ord(known[i])
flag[-1] = ord('}')

s = Solver()

# Flag is probably printable ascii text
for i in range(7, 24):
    s.add(flag[i] <= 127)
    s.add(flag[i] >= 0x20)

first8 = 0
for i in range(8):
    first8 += flag[i]

s.add(first8 == 877)
s.add(flag[13] == flag[16])
s.add(flag[13] == flag[21])
s.add(flag[19] == 7 * (flag[12] - flag[13]) / 2)
s.add(flag[13] + flag[12] == flag[16] + flag[15])
s.add(flag[7] + flag[8] + flag[9] - 51 == 2 * flag[9])
s.add(flag[8] == flag[20])
s.add(flag[10] + flag[11] - flag[17] - flag[18] == flag[10] - flag[17])
s.add(flag[20] == 51)
s.add(flag[22] + flag[23] == flag[22] * 2)
s.add(flag[9] - flag[17] == 40)
s.add(flag[10] - flag[17] - 6 == 0)
s.add(flag[2] - flag[11] == 50)
s.add(flag[24] - flag[12] == 10)
s.add(flag[13] + flag[15] == 2 * flag[14])
s.add(flag[23] == flag[22])
s.add(3 * flag[23] == flag[2])

# prints all possible solutions
while s.check() == z3.sat:
    solution = "False"
    m = s.model()

    candidate_key = ""
    for ob in sorted([(d, chr(m[d].as_long())) for d in m], key = lambda x: int(str(x[0])[5:-1])):
        candidate_key += ob[1]
    print(candidate_key)

    for i in m:
        solution = f"Or(({i} != {m[i]}), {solution})"
    f2 = eval(solution)
    s.add(f2)

This stackoverflow post was helpful when generating all possible solutions. Output:

➜  tetris python script.py 
t3tR1sOasOL1~3O!!
t3tR1sQbsQL1w3Q!!
t3tR1sinsiL1#3i!!
t3tR1sScsSL1p3S!!
t3tR1sgmsgL1*3g!!
t3tR1selseL113e!!
t3tR1sUdsUL1i3U!!
t3tR1sckscL183c!!
t3tR1sWesWL1b3W!!
t3tR1sYfsYL1[3Y!!
t3tR1s[gs[L1T3[!!
t3tR1sajsaL1?3a!!
t3tR1s_is_L1F3_!!
t3tR1s]hs]L1M3]!!

Flag: bucket{t3tR1s_is_L1F3_!!}

Search 1 (390 Points, MEDIUM)

This was a challenge on the RSA encryption algorithm. Let’s quickly refresh ourselves of how RSA works.

1. Choose two large prime numbers p and q.
2. Compute n = p * q.
3. Compute l = tot(n) where tot() is Euler’s Totient Function.
4. Choose an integer e that is coprime to l, usually 65537. Use as public key to encrypt data.
5. Compute d which is the modular inverse of e in mod l. Use as private key to decrypt data. To break RSA, we need to find the private key d to decrypt encrypted messages.

The challenge source code in python is shown below.

from Crypto.Util.number import getPrime, inverse, bytes_to_long
from string import ascii_letters, digits
from random import choice

m = open("flag.txt", "rb").read()
p = getPrime(128)
q = getPrime(128)
n = p * q
e = 65537
l = (p-1)*(q-1)
d = inverse(e, l)

m = pow(bytes_to_long(m), e, n)
print(m)
print(n)
leak = (p-2)*(q-2)
print(leak)

The encrypted message m, the product of primes n, and leak is printed out. While factorizing a product of two primes is difficult, factorizing leak or (p - 2) * (q - 2), which is likely a composite number, is easier. We can simply visit factordb, to ask for its prime factors. Given the prime factors of leak, we can now calculate all the possible values that p-2 and q-2 could be, and just check if (p-2) + 2 and (q-2) + 2 multiplies to n. When we find the two prime numbers p and q, we can directly find the private key d and decrypt the flag.

from Crypto.Util.number import inverse, long_to_bytes

m = 31926322181829320440867795572367461263072186839164468046130653120398920483443
n = 85287700174252437367320413787230245045356371367637489816407419259414268664923
p2q2 = 85287700174252437367320413787230245044188198738240577433424443515248092829335

# factordb
p2q2_fs = [5, 7, 7, 13, 31, 109, 317, 270797, 1618679, 9701172463, 101070869899, 239075830492847, 243298274979203162441]

for i in range(2 ** len(p2q2_fs)):
    cs = bin(i)[2:].rjust(len(p2q2_fs), "0")
    p = 1
    for j in range(len(p2q2_fs)):
        if cs[j] == '1':
            p *= p2q2_fs[j]
    q = p2q2 // p

    p += 2
    q += 2
    if p * q == n:
        print("FOUND")
        e = 65537
        l = (p-1)*(q-1)
        d = inverse(e, l)

        print(long_to_bytes(pow(m, d, n)))

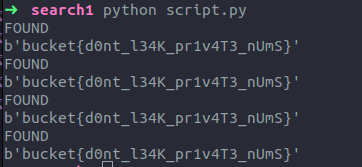
Flag: bucket{d0nt_l34K_pr1v4T3_nUmS}

Search 0 (380 Points, EASY)

This was another challenge on the RSA encryption algorithm. Check the writeup on Search 1 directly above for a refresher on RSA.

The challenge source code is as follows:

from Crypto.Util.number import getPrime, inverse, bytes_to_long
from string import ascii_letters, digits
from random import choice

m = open("flag.txt", "rb").read()
p = getPrime(128)
q = getPrime(128)
n = p * q
e = 65537
l = (p-1)*(q-1)
d = inverse(e, l)

m = pow(bytes_to_long(m), e, n)
print(m)
print(n)

p = "{0:b}".format(p)
for i in range(0,108):
    print(p[i], end="")

The server prints out the first 108 bits of the prime number p. We can easily brute force the remaining 20 bits, as 2 ** 20 is only around 1 million possible values. If the guessed value of p can divide n without remainders, we have found our two primes, and we can decrypt the flag.

from Crypto.Util.number import inverse, long_to_bytes

m = 4773465454870448875280141014802685313842148221787067779667635969253406960844
n = 71642450464029575733782514982146983097301804657621423739939506682546405443261
pt = int("110001010000010100101011111010010010000000110111000100101001010100110111010100100110010000101101110000101011", 2) << 20
for i in range(1 << 20):
    p = pt + i
    if n % p == 0:
        print("FOUND")
        q = n // p
        e = 65537
        l = (p - 1) * (q - 1)
        d = inverse(e, l)

        print(long_to_bytes(pow(m, d, n)))

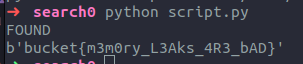
Flag: bucket{m3m0ry_L3Aks_4R3_bAD}